Solving Recurrence Relations

Recurrence relations, also called recursion, are functions that use previous values to calculate the next one. A famous example is the Fibonacci sequence,

where the sequence starts with f(0) = 1 and f(1) = 1.
It turns out that the Fibonacci sequence can be expressed in closed form, without using recursion.

where phi is the golden ratio and psi is its conjugate.


How to find the closed form expression?
In computer science undergraduate classes, students are taught to use induction to prove closed form solutions of recursions. This strategy requires you to guess the closed form. Guessing works on very simple recursions, but becomes unfeasible for anything more complicated.
The Fibonacci sequence cannot be solved using this technique. Instead, there is a systematic way of solving recurrence relations.
Introducing generating functions…
A generating function is a function defined on a infinite series. For example, the geometric series.

When we use these series as generating functions, we don’t care about what values x is going to take. We also don’t care about where it converges. We only care about the ordering of powers of x and the coefficients of powers of x.
The overall strategy consists of bringing recursions into generating functions, then extracting a closed form expression.


Start with writing the recursion as a function.

Build a generating function with the recursion. In this case, we use a ordinary generating function. See other kinds.
Substitute a_n into the generating function and add the base cases of the recursion.

Finally, using calculus and properties of series, we collapse A(x) back into a sum. The closed form solution is b_n.
Let’s do an example!
Example: Recursive addition
Consider this simple recursion. With base case, a_0 = 0.
This is none other than a_n = n, but let’s use generating functions as an example.
Since the recursion is already expressed with a_n isolated on one side, we can build the generating function right away.

The goal while at the generating functions level is to eliminate all recursive values of the original function. We do this by isolating recursive values and shifting the summation indices.


Now we isolate A(x) and expand the expression back into a series. The closed form solution would be the coefficients.
The brute force approach to expand A(x) back into a power series would be to use Taylor expansion. But since we know the sum of a geometric series, we can leverage that result by using derivatives. Alternatively, we could use partial fraction decomposition and add everything back together.
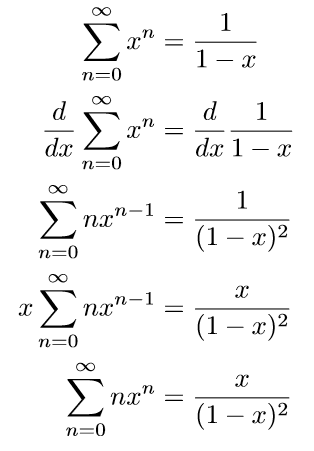

So we proved that a_n = a_{n-1} + 1 = n where a_0 = 0. That took quite some gymnastics to do!
The good news is that the method of generating functions is systematic and has no guessing, unlike guessing and checking with induction. Thus, it can be used to solve any kind of recursion, as long as you know how to wrestle with power series.
